Period-doubling bifurcation

In mathematics, a period doubling bifurcation in a discrete dynamical system is a bifurcation in which the system switches to a new behavior with twice the period of the original system. Period doubling bifurcations can also occur in continuous dynamical systems, namely when a new limit cycle emerges from an existing limit cycle, and the period of the new limit cycle is twice that of the old one.

Contents

Examples

Consider the following logistical map for a modified Phillips curve:

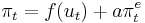
\pi_{t} = f(u_{t}) %2B a \pi_{t}^e
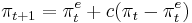
\pi_{t%2B1} = \pi_{t}^e %2B c (\pi_{t} - \pi_{t}^e)
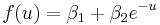
f(u) = \beta_{1} %2B \beta_{2} e^{-u} \,
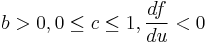
b > 0, 0 \leq c \leq 1, \frac {df} {du} < 0

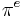where \pi is the actual inflation, \pi^e is the expected inflation, u is the level of unemployment, and 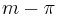m - \pi is the money supply growth rate. Keeping 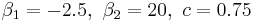\beta_{1} = -2.5, \ \beta_{2} = 20, \ c = 0.75 and varying b, the system undergoes period doubling bifurcations, and after a point becomes chaotic, as illustrated in the bifurcation diagram on the right.

Period-halving bifurcation

A period halving bifurcation in a dynamical system is a bifurcation in which the system switches to a new behavior with half the period of the original system. A series of period-halving bifurcations leads the system from chaos to order.

See also

External links